Abstract
The formation of antihydrogen atoms from antiprotons injected into a positron plasma is simulated, focussing on the fraction that fulfil the conditions necessary for confinement of anti-atoms in a magnetic minimum trap. Trapping fractions of around 10−4 are found under conditions similar to those used in recent experiments, and in reasonable accord with their results. We have studied the behaviour of the trapped fraction at various positron plasma densities and temperatures and found that collisional effects play a beneficial role via a redistribution of the antihydrogen magnetic moment, allowing enhancements of the yield of low-field seeking states that are amenable to trapping.
Export citation and abstract BibTeX RIS

Original content from this work may be used under the terms of the Creative Commons Attribution 3.0 licence. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
1. Introduction
Recent years have seen major experimental advances in the production and trapping of antihydrogen, 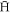 , the positron (e+)−antiproton (
, the positron (e+)−antiproton (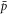 ) bound state (see e.g., the reviews [1–4]), which have facilitated the first determinations of some of its properties [5–9]. Indeed, such measurements were only feasible due to the capability to hold ground state
) bound state (see e.g., the reviews [1–4]), which have facilitated the first determinations of some of its properties [5–9]. Indeed, such measurements were only feasible due to the capability to hold ground state 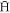 in a magnetic minimum neutral atom trap for periods of many minutes [10–12] to allow interaction with applied electric fields, or microwave or laser radiation. These experiments were typically performed with between 1 and 10
in a magnetic minimum neutral atom trap for periods of many minutes [10–12] to allow interaction with applied electric fields, or microwave or laser radiation. These experiments were typically performed with between 1 and 10 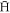 atoms in the trap.
atoms in the trap.
The depth of a magnetic trap for ground state 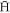 is around 0.7 K per Tesla of magnetic field change. In the ALPHA experiment, for instance, this amounts to around 0.5 K [13], and it is unlikely, given the field and space constraints on such apparatus, that traps significantly deeper than this will be available soon. As such, attention has focussed on maximising the trapped antihydrogen yield by preparing cold, dense clouds of positrons and antiprotons, and devising means of mixing them to form
is around 0.7 K per Tesla of magnetic field change. In the ALPHA experiment, for instance, this amounts to around 0.5 K [13], and it is unlikely, given the field and space constraints on such apparatus, that traps significantly deeper than this will be available soon. As such, attention has focussed on maximising the trapped antihydrogen yield by preparing cold, dense clouds of positrons and antiprotons, and devising means of mixing them to form 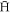 whilst maintaining their low temperature. Techniques such as evaporative [14] and adiabatic [15] cooling have been developed, whilst compression techniques (see, e.g., [16, 17]) have allowed the density and radial extent of the clouds to be carefully manipulated. Whilst this has led to marked improvements in
whilst maintaining their low temperature. Techniques such as evaporative [14] and adiabatic [15] cooling have been developed, whilst compression techniques (see, e.g., [16, 17]) have allowed the density and radial extent of the clouds to be carefully manipulated. Whilst this has led to marked improvements in 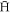 trapping efficiencies (here, defined as the number of
trapping efficiencies (here, defined as the number of 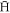 trapped per injected
trapped per injected 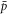 ), from about 5 × 10−6 in the earliest work [10] to over 10−4 in a recent study [18], it is clear that many measurements will benefit markedly from increases in the yield of trapped
), from about 5 × 10−6 in the earliest work [10] to over 10−4 in a recent study [18], it is clear that many measurements will benefit markedly from increases in the yield of trapped 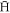 .
.
In most of the  experiments performed to date the positron density (ne) and temperature (T) conditions are such that formation of the anti-atom is dominated by the three-body collision reaction,
experiments performed to date the positron density (ne) and temperature (T) conditions are such that formation of the anti-atom is dominated by the three-body collision reaction,

(see, e.g., [1] for a discussion). Theoretical and computational studies of this process have, as reviewed by Robicheaux [19], been undertaken for some time and have elucidated how some of the underlying features of this reaction (such as the production of weakly bound states, and the sensitivity to the positron plasma temperature) affect the experimental observations. In previous work [20, 21], we have contributed to this endeavour and have found, in particular, that the 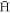 that is observed experimentally is the result of a cycle of formation and break-up (i.e., the reverse of reaction (1)) processes which also involve radial transport of the
that is observed experimentally is the result of a cycle of formation and break-up (i.e., the reverse of reaction (1)) processes which also involve radial transport of the  when they are bound to a positron.
when they are bound to a positron.
Here we extend that work to consider the properties of the formed  , and in particular those that govern whether the anti-atom can be held in a shallow neutral atom trap. The remainder of the article is organised as follows: in section 2 we give a description of our calculational methods, and the criteria we apply to judge whether the
, and in particular those that govern whether the anti-atom can be held in a shallow neutral atom trap. The remainder of the article is organised as follows: in section 2 we give a description of our calculational methods, and the criteria we apply to judge whether the 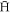 is potentially trappable. Our main results and discussion are given in section 3, with concluding remarks in section 4.
is potentially trappable. Our main results and discussion are given in section 3, with concluding remarks in section 4.
2. Method
Details of our simulation method have been published previously [20, 21], and as such we concentrate mainly on aspects that inform the discussion herein. Classical trajectories of 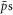 and e+s were calculated using the full equations of motion in a combination of magnetic (axial 1 Tesla) and electric (self charge of the positron plasma) fields. This treatment does not include the magnetic fields from the atom trap which are close to zero at the position where antihydrogen is formed in an experiment, and vary little across the physical extent of the positron plasma [20]. The
and e+s were calculated using the full equations of motion in a combination of magnetic (axial 1 Tesla) and electric (self charge of the positron plasma) fields. This treatment does not include the magnetic fields from the atom trap which are close to zero at the position where antihydrogen is formed in an experiment, and vary little across the physical extent of the positron plasma [20]. The 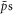 were initialised from a thermal distribution, with the same temperature as the e+ plasma, with the latter modelled as an infinitely long cylinder with a radius of 1 mm. Temperature effects on ne were neglected as they are very small over the range covered here, and as a result the density was modelled as constant out to 1 mm, whereupon it discontinuously dropped to zero. The electric field, E, inside the plasma is given by
were initialised from a thermal distribution, with the same temperature as the e+ plasma, with the latter modelled as an infinitely long cylinder with a radius of 1 mm. Temperature effects on ne were neglected as they are very small over the range covered here, and as a result the density was modelled as constant out to 1 mm, whereupon it discontinuously dropped to zero. The electric field, E, inside the plasma is given by
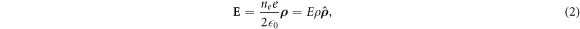
where 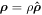 is the radial coordinate with the origin at the trap axis, and e and
is the radial coordinate with the origin at the trap axis, and e and  0 have their usual meanings. This field, in combination with the magnetic field, B, perpendicular to it and along the trap axis, gives rise to a rotation of both charged particle species around that axis, with the speed of rotation given by
0 have their usual meanings. This field, in combination with the magnetic field, B, perpendicular to it and along the trap axis, gives rise to a rotation of both charged particle species around that axis, with the speed of rotation given by
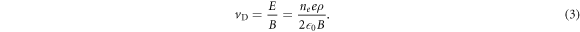
When the temperature of the charged particles is cited herein, it is the temperature in this rotating frame, and since vD increases with both ne and the radial position in the trap, it may be expected that the probability of 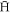 trapping will be reduced with increases in either parameter.
trapping will be reduced with increases in either parameter.
There are two main reasons for the use of the simplified description of the plasma outlined above. The first is due to computational constraints, which necessitates that the number of parameters be limited. More significantly, though, is that we hope to elucidate some of the general features of  formation, whereas a more detailed description would involve quantities such as plasma shapes, and trapping fields and configurations, that can vary considerably from experiment to experiment, and also over time within a given experiment. We believe that our simulations capture the essential generic features of
formation, whereas a more detailed description would involve quantities such as plasma shapes, and trapping fields and configurations, that can vary considerably from experiment to experiment, and also over time within a given experiment. We believe that our simulations capture the essential generic features of  formation in the ALPHA [10–12], ATRAP [22] and ASACUSA [23, 24] experiments (though the latter do not seek to trap the anti-atom).
formation in the ALPHA [10–12], ATRAP [22] and ASACUSA [23, 24] experiments (though the latter do not seek to trap the anti-atom).
Since the e+ plasma is modelled as an infinitely long cylinder, the effect of the arrested 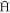 formation due to repeated cycles of
formation due to repeated cycles of 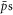 leaving and re-entering the plasma [25] is not included. This is justified since the low energy
leaving and re-entering the plasma [25] is not included. This is justified since the low energy 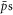 follow the magnetic field lines and re-enter the plasma in the same state as they left it. Furthermore, any
follow the magnetic field lines and re-enter the plasma in the same state as they left it. Furthermore, any 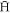 leaving the plasma axially is also missed in this approximation. In [20] it was found that, when radial
leaving the plasma axially is also missed in this approximation. In [20] it was found that, when radial 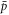 drift due to
drift due to 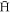 formation was accounted for, the
formation was accounted for, the 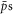 escaped the plasma radially within ∼10 ms at relevant values of ne and T, though before this occurs they have typically undergone many cycles of
escaped the plasma radially within ∼10 ms at relevant values of ne and T, though before this occurs they have typically undergone many cycles of 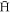 formation and subsequent ionisation. Since
formation and subsequent ionisation. Since  formation must occur within the e+ plasma, the relevant measure to estimate the ratio of radially to axially escaping
formation must occur within the e+ plasma, the relevant measure to estimate the ratio of radially to axially escaping 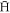 , is the time between the
, is the time between the 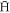 formation event in the last of these cycles, and the time when this
formation event in the last of these cycles, and the time when this 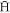 leaves the plasma. We have been able to extract these from our simulations, and found that the typical time scale (at T = 10 K) varies from ∼1 μs at the highest density used in our simulations (ne = 1015 m−3) and up to ∼5 μs at our lowest density (ne = 1013 m−3). During 1 μs a 10 K
leaves the plasma. We have been able to extract these from our simulations, and found that the typical time scale (at T = 10 K) varies from ∼1 μs at the highest density used in our simulations (ne = 1015 m−3) and up to ∼5 μs at our lowest density (ne = 1013 m−3). During 1 μs a 10 K 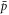 will on average travel ∼0.2 mm axially. Since typical positron plasmas have lengths ∼cm, this confirms that most stable
will on average travel ∼0.2 mm axially. Since typical positron plasmas have lengths ∼cm, this confirms that most stable 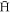 should escape radially. This has also been observed experimentally (see the axial distributions of annihilation events in [26, 27]). Furthermore, any unstable
should escape radially. This has also been observed experimentally (see the axial distributions of annihilation events in [26, 27]). Furthermore, any unstable  which leaves a finite length plasma axially and is field ionised results in a
which leaves a finite length plasma axially and is field ionised results in a 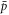 which either follows a magnetic field line back to the plasma, or becomes trapped in the side wells [28], in which case it is lost for the purposes of
which either follows a magnetic field line back to the plasma, or becomes trapped in the side wells [28], in which case it is lost for the purposes of 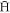 formation.
formation.
Whilst previous work focussed on the radial transport of  [20], here the state of the
[20], here the state of the 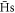 leaving the plasma radially is examined. Our goal is to estimate the number of
leaving the plasma radially is examined. Our goal is to estimate the number of 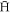 with properties which may allow them to be magnetically trapped, per
with properties which may allow them to be magnetically trapped, per 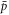 entering the plasma. It is therefore vital to be able to separate truly bound
entering the plasma. It is therefore vital to be able to separate truly bound 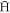 states from situations where a e+ just happened to be close to a
states from situations where a e+ just happened to be close to a 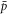 at the moment the latter crossed the outer limit of the plasma. Due to the presence of the external fields, the binding energy is an ill-defined property for such loosely bound objects. Instead, an operational definition of what constitutes an
at the moment the latter crossed the outer limit of the plasma. Due to the presence of the external fields, the binding energy is an ill-defined property for such loosely bound objects. Instead, an operational definition of what constitutes an 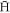 is used: if, in the absence of further collisions with positrons, the
is used: if, in the absence of further collisions with positrons, the 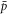 and e+ remain together for a further 'wait time' of 1 μs, we count this as an
and e+ remain together for a further 'wait time' of 1 μs, we count this as an  event. During this period the 1 T axial magnetic field is still present, but the radial electric field is changed to be ∝ρ−1, as appropriate outside a cylindrical charged plasma. Further, in order to sift the
event. During this period the 1 T axial magnetic field is still present, but the radial electric field is changed to be ∝ρ−1, as appropriate outside a cylindrical charged plasma. Further, in order to sift the 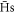 which are bound strongly enough to survive the fields in the trap, an axial 10 V cm−1 electric field is applied (unless otherwise specified) during the wait time. We do not include the actual electric field from any particular configuration of trap electrodes, as we do not follow the
which are bound strongly enough to survive the fields in the trap, an axial 10 V cm−1 electric field is applied (unless otherwise specified) during the wait time. We do not include the actual electric field from any particular configuration of trap electrodes, as we do not follow the 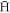 trajectories outside the plasma. This field, chosen to be parallel to B, is typical of those found in the charged particle traps used in
trajectories outside the plasma. This field, chosen to be parallel to B, is typical of those found in the charged particle traps used in 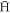 experimentation. A simple estimate (see, e.g., [29]) reveals that
experimentation. A simple estimate (see, e.g., [29]) reveals that 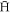 states with binding energies (in units of kelvin) around
states with binding energies (in units of kelvin) around 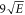 , with E in V cm−1, will be field ionised, which corresponds to states bound by up to ∼28 K. Below, we will examine how this criterion affects our final result.
, with E in V cm−1, will be field ionised, which corresponds to states bound by up to ∼28 K. Below, we will examine how this criterion affects our final result.
We refer to the fraction of 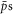 resulting in
resulting in 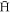 which survives this treatment as the
which survives this treatment as the  -fraction,
-fraction, 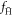 . Radiative de-excitation processes which may contribute to the formation of stable
. Radiative de-excitation processes which may contribute to the formation of stable 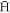 , are not included, as these are not important during the first stages of
, are not included, as these are not important during the first stages of 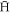 formation [30, 31].
formation [30, 31].
Amongst the identified stable 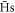 , further cuts are applied to determine the number in a state suitable for magnetic trapping. Since we do not consider the radiative cascade of the
, further cuts are applied to determine the number in a state suitable for magnetic trapping. Since we do not consider the radiative cascade of the 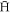 after leaving the plasma, its state on exit is examined to determine whether it can be trapped. First the direction of the magnetic moment is considered. An
after leaving the plasma, its state on exit is examined to determine whether it can be trapped. First the direction of the magnetic moment is considered. An 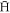 atom can only be trapped if its potential energy, Ep (the energy of the atom-magnetic field interaction), increases with magnetic field strength, i.e., it is in a low-field seeking state. In the approximation of an infinitely heavy antiproton, so that the coupling to the centre-of-mass motion can be ignored, the variation of Ep with magnetic field for a particle of mass me is given by [32] (with the brackets signifying time averages),
atom can only be trapped if its potential energy, Ep (the energy of the atom-magnetic field interaction), increases with magnetic field strength, i.e., it is in a low-field seeking state. In the approximation of an infinitely heavy antiproton, so that the coupling to the centre-of-mass motion can be ignored, the variation of Ep with magnetic field for a particle of mass me is given by [32] (with the brackets signifying time averages),
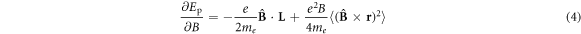
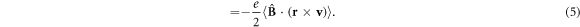
Here r is the position of the e+, relative to the 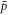 , v is the e+ velocity in the frame of the atom and L is the canonical angular momentum, which is conserved along the magnetic field in the limit of infinite
, v is the e+ velocity in the frame of the atom and L is the canonical angular momentum, which is conserved along the magnetic field in the limit of infinite 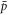 mass (though it is only approximately conserved when couplings between the centre-of-mass and internal motions are included). If
mass (though it is only approximately conserved when couplings between the centre-of-mass and internal motions are included). If 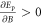 , then the
, then the 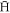 is a low-field seeker which can be trapped magnetically. The second term in (4) is not conserved, but will instead be reduced as r lowers during the cascade to more deeply bound states. Therefore, the first condition for an
is a low-field seeker which can be trapped magnetically. The second term in (4) is not conserved, but will instead be reduced as r lowers during the cascade to more deeply bound states. Therefore, the first condition for an 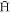 to be trappable is that the first term in (4) is required to be positive, i.e.
to be trappable is that the first term in (4) is required to be positive, i.e. 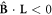 . As was pointed out by Robicheaux [32] the direction of L is not random, and the cyclotron rotation of the positrons will predominantly select initial
. As was pointed out by Robicheaux [32] the direction of L is not random, and the cyclotron rotation of the positrons will predominantly select initial 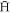 states with
states with 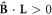 : i.e., the wrong sign for the purpose of trapping. Thus, this condition reduces the number of
: i.e., the wrong sign for the purpose of trapping. Thus, this condition reduces the number of 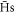 available for trapping by more than a factor of two.
available for trapping by more than a factor of two.
The final condition for trapping is the requirement that the kinetic energy of the 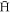 must be low enough for it to be confined by the atom trap, which for ALPHA is around 0.5 K [10]. However, since typical trapping fractions are only around 1
must be low enough for it to be confined by the atom trap, which for ALPHA is around 0.5 K [10]. However, since typical trapping fractions are only around 1 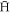 per 103 to 104
per 103 to 104 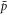 (or even lower fractions at the highest temperature and lowest densities in our simulations) this condition would require the running of very many trajectories to acquire useful statistics. As a compromise between computational time and statistical uncertainty we have run about 20 000
(or even lower fractions at the highest temperature and lowest densities in our simulations) this condition would require the running of very many trajectories to acquire useful statistics. As a compromise between computational time and statistical uncertainty we have run about 20 000 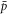 trajectories per parameter setting. As a result the 0.5 K equivalent energy criterion was loosened, to require that the kinetic energy of the
trajectories per parameter setting. As a result the 0.5 K equivalent energy criterion was loosened, to require that the kinetic energy of the  was less than 2 K. For a thermal distribution with a temperature in the range 10–30 K, 13% of the anti-atoms with kinetic energy <2 K will satisfy <0.5 K.
was less than 2 K. For a thermal distribution with a temperature in the range 10–30 K, 13% of the anti-atoms with kinetic energy <2 K will satisfy <0.5 K.
To further improve the computational speed, we froze the internal states of 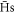 with binding energies exceeding 300 K, and only followed their ballistic trajectory until they left the plasma. In addition we used a softening of the Coulomb potential, i.e.,
with binding energies exceeding 300 K, and only followed their ballistic trajectory until they left the plasma. In addition we used a softening of the Coulomb potential, i.e.,
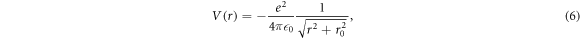
where r0 is a constant that removes the singularity as 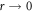 . After testing, we determined that our results were stable using r0 = 2 × 10−8 m.
. After testing, we determined that our results were stable using r0 = 2 × 10−8 m.
The 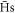 which satisfy the conditions of stability, magnetic moment and kinetic energy listed above constitute our definition of trappable
which satisfy the conditions of stability, magnetic moment and kinetic energy listed above constitute our definition of trappable  , as a fraction of the injected
, as a fraction of the injected  , ftrap.
, ftrap.
All of the simulations presented are for an axial magnetic field of 1 T. Three different temperatures of the positron plasma, 10, 15 and 30 K have been investigated for a number of plasma densities between ne = 1013 m−3 and ne = 1015 m−3. For most of our simulations the 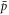 trajectories were initialised on the axis of the trap, defined as ρstart = 0.
trajectories were initialised on the axis of the trap, defined as ρstart = 0.
3. Results and discussion
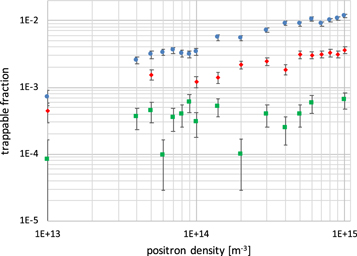
The principal results of our investigation are summarised in figure 1 which shows the trappable fraction, ftrap, across the different parameter ranges considered. As expected, lower positron temperatures strongly favour 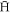 trapping. However, the dependence upon ne is unexpected since increases in the parameter do not show a reduction of ftrap. As argued in section 2, since vD increases with density, one would expect the kinetic energy in the stationary frame to increase proportionally, thereby reducing the probability of trapping. A partial reason for the absence of this reduction is that the
trapping. However, the dependence upon ne is unexpected since increases in the parameter do not show a reduction of ftrap. As argued in section 2, since vD increases with density, one would expect the kinetic energy in the stationary frame to increase proportionally, thereby reducing the probability of trapping. A partial reason for the absence of this reduction is that the 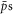 were injected on the axis of the trap, i.e. at ρstart = 0. Here, if stable
were injected on the axis of the trap, i.e. at ρstart = 0. Here, if stable  is formed before the
is formed before the 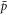 has drifted away from its initial radius, the kinetic energy contribution from vD will vanish.
has drifted away from its initial radius, the kinetic energy contribution from vD will vanish.
Figure 1. The fraction of 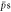 giving trappable
giving trappable 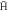 (according to the definitions given in section 2) as a function of positron density, for the temperatures 10 K (blue circles), 15 K (red diamonds) and 30 K (green squares). The
(according to the definitions given in section 2) as a function of positron density, for the temperatures 10 K (blue circles), 15 K (red diamonds) and 30 K (green squares). The 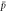 trajectories were initialised on the axis of the trap. Error bars show uncertainties proportional to
trajectories were initialised on the axis of the trap. Error bars show uncertainties proportional to 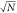 , with N the total trapped number.
, with N the total trapped number.
Download figure:
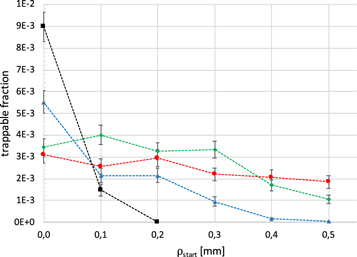
Standard image High-resolution imageAccordingly, we have examined ftrap as a function of injection radius, and the results for T = 10 K are shown in figure 2. Data for the higher temperatures show similar features, but with poorer statistics. The results show that at low ne, ftrap is largely independent of ρstart, whilst at high densities trapping is drastically reduced when antiprotons are injected away from the axis. Thus, the form of figure 1, if the effect of ρstart > 0 is included, will depend on how close to the axis the 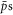 are injected in any particular experiment. We can estimate at which density effects from ρstart > 0 become important by assuming that all
are injected in any particular experiment. We can estimate at which density effects from ρstart > 0 become important by assuming that all 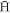 form at ρstart, and comparing vD to the thermal velocity (in three dimensions) as,
form at ρstart, and comparing vD to the thermal velocity (in three dimensions) as,
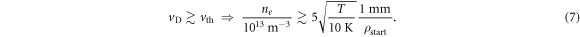
This estimate agrees quite well with the data in figure 2. Thus, we conclude that, in a real experiment, ftrap will be reduced compared to the results shown in figure 1 for ne ≳ 1014 m−3, and that the size of this effect will depend on the particular conditions and can be estimated using the information given in figure 2.
Figure 2. The fraction of 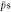 giving trappable
giving trappable 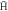 as a function of injection radius for T = 10 K and different densities: ne = 5 × 1013 m−3 (red circles), ne = 1014 m−3 (green diamonds), ne = 2 × 1014 m−3 (blue triangles) and ne = 5 × 1014 m−3 (black squares). For ne = 1015 m−3 the trappable fraction dropped below 10−4 when ρstart = 0.1 mm.
as a function of injection radius for T = 10 K and different densities: ne = 5 × 1013 m−3 (red circles), ne = 1014 m−3 (green diamonds), ne = 2 × 1014 m−3 (blue triangles) and ne = 5 × 1014 m−3 (black squares). For ne = 1015 m−3 the trappable fraction dropped below 10−4 when ρstart = 0.1 mm.
Download figure:
Standard image High-resolution imageWe have also investigated how sensitive our results for ftrap are to the criteria we imposed when defining what constitutes a bound 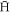 . That is, we varied the strength of the axial electric field applied during the 1 μs wait period from 1 to 15 V cm−1. The results are shown in figure 3. We conclude that, within reasonable limits, our choice of electric field does not affect our results beyond the statistical fluctuations. However, a more detailed analysis revealed that at low densities
. That is, we varied the strength of the axial electric field applied during the 1 μs wait period from 1 to 15 V cm−1. The results are shown in figure 3. We conclude that, within reasonable limits, our choice of electric field does not affect our results beyond the statistical fluctuations. However, a more detailed analysis revealed that at low densities 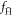 is influenced by this choice, though this effect does not carry over into ftrap. Our interpretation is that those
is influenced by this choice, though this effect does not carry over into ftrap. Our interpretation is that those 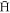 which have magnetic moments pointing in the direction which allows trapping, have undergone more or stronger collisions, which has also increased their binding energy beyond the average.
which have magnetic moments pointing in the direction which allows trapping, have undergone more or stronger collisions, which has also increased their binding energy beyond the average.
Figure 3. The fraction of 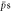 giving trappable
giving trappable 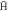 as a function of positron plasma density for T = 10 K and different axial electric fields applied during the 'wait' period: E = 1 V cm−1 (blue circles), E = 2 V cm−1 (red diamonds), E = 5 V cm−1 (green squares), E = 10 V cm−1 (black triangles) and E = 15 V cm−1 (purple crosses). (Note, for each density the data points are not independent, but result from the same simulation up to the point where the electric field is applied. It is thus expected that the statistical errors will be correlated for the different electric fields.)
as a function of positron plasma density for T = 10 K and different axial electric fields applied during the 'wait' period: E = 1 V cm−1 (blue circles), E = 2 V cm−1 (red diamonds), E = 5 V cm−1 (green squares), E = 10 V cm−1 (black triangles) and E = 15 V cm−1 (purple crosses). (Note, for each density the data points are not independent, but result from the same simulation up to the point where the electric field is applied. It is thus expected that the statistical errors will be correlated for the different electric fields.)
Download figure:
Standard image High-resolution imageWe now take a closer look at how the three criteria for ftrap, as defined in section 2, combine to create the overall results shown in figure 1. First, figure 4 shows 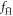 , i.e., the fraction of
, i.e., the fraction of 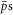 forming stable
forming stable  . These data have several interesting features. We do not find a strong dependence on temperature. At densities below ∼2 × 1014 m−3
. These data have several interesting features. We do not find a strong dependence on temperature. At densities below ∼2 × 1014 m−3 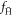 steadily increases with ne. This is followed by a maximum, after which
steadily increases with ne. This is followed by a maximum, after which 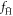 drops for all temperatures. Our interpretation is that the form of these curves is a result of the binding energy of the nascent
drops for all temperatures. Our interpretation is that the form of these curves is a result of the binding energy of the nascent 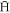 . Our procedure for selecting stable
. Our procedure for selecting stable 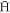 will remove those with a binding energy too low to survive the electric fields in the trap. The binding energy that can be attained by an
will remove those with a binding energy too low to survive the electric fields in the trap. The binding energy that can be attained by an 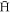 before it leaves the plasma depends on the number of collisions with positrons it has undergone, and as result it is expected to increase with plasma density. The dependence on temperature is more complicated because a higher temperature will both lower the number of collisions (since the
before it leaves the plasma depends on the number of collisions with positrons it has undergone, and as result it is expected to increase with plasma density. The dependence on temperature is more complicated because a higher temperature will both lower the number of collisions (since the 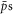 form
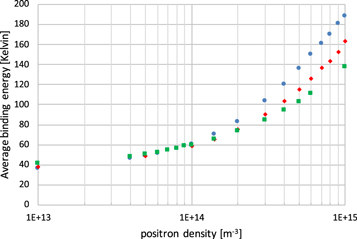
form 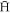 less frequently), but also increase the energy exchange per collision, thus resulting in two opposing effects. Figure 5 shows the average
less frequently), but also increase the energy exchange per collision, thus resulting in two opposing effects. Figure 5 shows the average 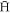 binding energy, after applying the stability criteria. The data confirm our qualitative expectations. In particular it is notable that at the lower densities there is little temperature dependence, and that the binding energy increases with ne. Thus, a larger fraction of the
binding energy, after applying the stability criteria. The data confirm our qualitative expectations. In particular it is notable that at the lower densities there is little temperature dependence, and that the binding energy increases with ne. Thus, a larger fraction of the 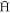 will be stable as ne increases, consistent with the low density region in figure 4. This effect will continue until a density has been reached where almost all the
will be stable as ne increases, consistent with the low density region in figure 4. This effect will continue until a density has been reached where almost all the 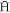 has a binding energy large enough to be stable. At this point it would be expected that the curves in figure 4 will level out.
has a binding energy large enough to be stable. At this point it would be expected that the curves in figure 4 will level out.
Figure 4. The fraction of 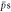 giving stable
giving stable 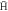 atoms (according to the definition in section 2) as a function of density. The temperatures are 10 K (blue circles), 15 K (red diamonds) and 30 K (green squares). The
atoms (according to the definition in section 2) as a function of density. The temperatures are 10 K (blue circles), 15 K (red diamonds) and 30 K (green squares). The 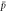 trajectories were initialised on the axis of the trap.
trajectories were initialised on the axis of the trap.
Download figure:
Standard image High-resolution imageFigure 5. The average binding energy of the 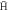 atoms formed. The temperatures are 10 K (blue circles), 15 K (red diamonds) and 30 K (green squares). Note that the internal state was frozen for atoms with binding energies exceeding 300 K. This may have a slight effect on the average binding energy at the highest densities (see also figure 6).
atoms formed. The temperatures are 10 K (blue circles), 15 K (red diamonds) and 30 K (green squares). Note that the internal state was frozen for atoms with binding energies exceeding 300 K. This may have a slight effect on the average binding energy at the highest densities (see also figure 6).
Download figure:
Standard image High-resolution imageHowever, as is evident, instead of a constant 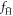 at high ne a temperature-dependent reduction is observed. To understand this feature we have to go beyond the average binding energy, and examine its distribution. Figure 6 compares the distribution of binding energies at densities of 1013, 1014 and 1015 m−3 at T = 10 K, revealing major differences.
at high ne a temperature-dependent reduction is observed. To understand this feature we have to go beyond the average binding energy, and examine its distribution. Figure 6 compares the distribution of binding energies at densities of 1013, 1014 and 1015 m−3 at T = 10 K, revealing major differences.
Figure 6. Distribution of binding energies for 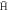 atoms leaving a 10 K positron plasma, for ne = 1015 m−3 (blue circles), ne = 1014 m−3 (yellow squares) and ne = 1013 m−3 (green triangles). The stability criteria (see text) for the
atoms leaving a 10 K positron plasma, for ne = 1015 m−3 (blue circles), ne = 1014 m−3 (yellow squares) and ne = 1013 m−3 (green triangles). The stability criteria (see text) for the 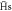 have been applied here.
have been applied here.
Download figure:
Standard image High-resolution imageThe 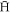 that are initially formed via reaction (1) typically possess a small binding energy. As they collide with positrons, a few of them trickle down to deeper binding energies, while others are ionised. One would therefore expect most
that are initially formed via reaction (1) typically possess a small binding energy. As they collide with positrons, a few of them trickle down to deeper binding energies, while others are ionised. One would therefore expect most 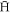 to have small binding energies, with a tail towards deeper binding developing with time, eventually forming a steady state [31]. This is what occurs at 1013m−3 and 1014 m−3, except that some of the
to have small binding energies, with a tail towards deeper binding developing with time, eventually forming a steady state [31]. This is what occurs at 1013m−3 and 1014 m−3, except that some of the 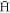 with binding energy ≲30 K have been removed by the electric field during the wait. This is consistent with the explanation given above of the linear increase for low densities.
with binding energy ≲30 K have been removed by the electric field during the wait. This is consistent with the explanation given above of the linear increase for low densities.
The distribution at 1015 m−3 is markedly different, with very few 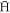 close to zero binding energy, and a broad maximum around 80 K. To understand this difference, it should be recalled that the distribution of binding energies is not a snapshot of all
close to zero binding energy, and a broad maximum around 80 K. To understand this difference, it should be recalled that the distribution of binding energies is not a snapshot of all  at some given time. Instead it is the distribution for those
at some given time. Instead it is the distribution for those 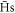 that have been radially transported across the outer radius of the plasma, independently of when or where they were initially formed. As discussed in [20], two mechanisms for radial transport need to be considered: (i) thermal diffusion of the
that have been radially transported across the outer radius of the plasma, independently of when or where they were initially formed. As discussed in [20], two mechanisms for radial transport need to be considered: (i) thermal diffusion of the 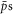 and (ii) radial jumps arising from antihydrogen formation. The relative importance of the two mechanisms depends on positron density and temperature, where vD < vth favours thermal diffusion, with the jump mechanism dominating in the opposite limit.
and (ii) radial jumps arising from antihydrogen formation. The relative importance of the two mechanisms depends on positron density and temperature, where vD < vth favours thermal diffusion, with the jump mechanism dominating in the opposite limit.
As can be seen from equation (7) and figure 2, at 1015 m−3 the drift velocity dominates over thermal motion over almost the entire plasma (except very close to the axis). As a consequence, the 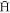 formation mechanism becomes important. At this density most of the stable
formation mechanism becomes important. At this density most of the stable 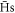 leaving the plasma were formed close to the axis, and then, while still bound, radially transported through the plasma and across its outer radius. During this jump, the
leaving the plasma were formed close to the axis, and then, while still bound, radially transported through the plasma and across its outer radius. During this jump, the  will collide with positrons, and only those which manage to attain a large binding energy will survive all the way. Any
will collide with positrons, and only those which manage to attain a large binding energy will survive all the way. Any 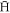 with a small binding energy is likely to ionise before it escapes the plasma, and will not contribute to the recorded distribution. Thus, the distribution obtained at 1015 m−3 is the result of a post-selection effect, where the radial transport mechanism selects the most deeply bound
with a small binding energy is likely to ionise before it escapes the plasma, and will not contribute to the recorded distribution. Thus, the distribution obtained at 1015 m−3 is the result of a post-selection effect, where the radial transport mechanism selects the most deeply bound  of all those formed.
of all those formed.
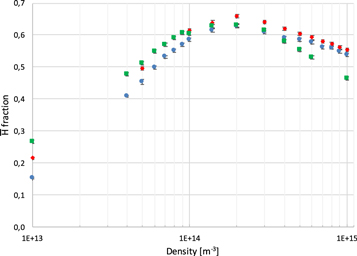
The trend at high densities in figure 4 (i.e., less stable 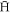 at elevated ne) goes against the trend in figure 1 (a roughly constant number of trappable
at elevated ne) goes against the trend in figure 1 (a roughly constant number of trappable 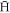 under similar conditions). To explain this difference we have examined the distribution of magnetic moments, and the results shown in figure 7 confirm the conclusion of Robicheaux [32] that
under similar conditions). To explain this difference we have examined the distribution of magnetic moments, and the results shown in figure 7 confirm the conclusion of Robicheaux [32] that 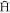 is preferentially formed in high-field seeking, untrapped states (though in that work the density dependence of the effect was not investigated). However, a trend towards a more beneficial distribution with increased density is also observed which compensates for the decline in the number of
is preferentially formed in high-field seeking, untrapped states (though in that work the density dependence of the effect was not investigated). However, a trend towards a more beneficial distribution with increased density is also observed which compensates for the decline in the number of 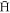 formed, resulting in a roughly constant ftrap at the higher temperatures in figure 1, while at 10 K there is a slow increase all the way up to ne = 1015 m−3. The reason for this effect is that, whilst the
formed, resulting in a roughly constant ftrap at the higher temperatures in figure 1, while at 10 K there is a slow increase all the way up to ne = 1015 m−3. The reason for this effect is that, whilst the 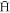 is formed in high-field seeking states, collisions with positrons (i.e., the same collisions which are necessary to stabilise the
is formed in high-field seeking states, collisions with positrons (i.e., the same collisions which are necessary to stabilise the 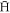 ) may change the direction of the magnetic moment. High density and low temperature result in more of these collisions, creating the trend in figure 7. We have confirmed this interpretation by following the time evolution of the magnetic moment of the last
) may change the direction of the magnetic moment. High density and low temperature result in more of these collisions, creating the trend in figure 7. We have confirmed this interpretation by following the time evolution of the magnetic moment of the last 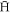 to be formed in a
to be formed in a 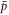 trajectory (i.e., the
trajectory (i.e., the 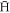 that finally escaped intact from the plasma), finding that the fraction of low-field seekers does indeed increase with time, and with a rate roughly proportional to ne.
that finally escaped intact from the plasma), finding that the fraction of low-field seekers does indeed increase with time, and with a rate roughly proportional to ne.
Figure 7. The fraction of stable 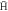 formed with B · Lz < 0, i.e., low-field seekers. The temperatures are 10 K (blue circles), 15 K (red diamonds) and 30 K (green squares).
formed with B · Lz < 0, i.e., low-field seekers. The temperatures are 10 K (blue circles), 15 K (red diamonds) and 30 K (green squares).
Download figure:
Standard image High-resolution image4. Concluding remarks
We have found that important aspects of 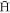 formation are qualitatively different depending on positron density, with low- and high-density regions separated at ne ∼ 2 × 1014 m−3. At the lower ne the number of trappable
formation are qualitatively different depending on positron density, with low- and high-density regions separated at ne ∼ 2 × 1014 m−3. At the lower ne the number of trappable 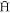 formed per injected
formed per injected 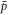 increases with density, whereas in the high-density region, this fraction is largely independent of ne at T ≳ 15 K, while it continues to grow slightly at 10 K.
increases with density, whereas in the high-density region, this fraction is largely independent of ne at T ≳ 15 K, while it continues to grow slightly at 10 K.
The condition imposed here that the kinetic energy must be less than 2 K for 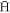 to be trapped makes ftrap very sensitive to positron temperature. Moreover, at high densities ftrap is reduced if the
to be trapped makes ftrap very sensitive to positron temperature. Moreover, at high densities ftrap is reduced if the 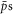 are injected away from the axis of the trap, while this effect is not present at low densities. The (binding energy) stability condition results in a largely temperature independent
are injected away from the axis of the trap, while this effect is not present at low densities. The (binding energy) stability condition results in a largely temperature independent  , increasing with density, at low densities. At high densities
, increasing with density, at low densities. At high densities 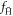 falls off again. The condition on the magnetic moment causes a reduction of ftrap considerably larger than a factor of two, however higher densities give more low-field seeking states, especially at the lower temperatures, due to the effects of positron collisions.
falls off again. The condition on the magnetic moment causes a reduction of ftrap considerably larger than a factor of two, however higher densities give more low-field seeking states, especially at the lower temperatures, due to the effects of positron collisions.
Finally, we make a comparison of our results with experimentally observed trapping fractions. In a recent publication by ALPHA [18], 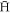 formation at T = 18 K and ne = 6.5 × 1013 m−3 (at the beginning of the mixing with antiprotons) resulted in,
formation at T = 18 K and ne = 6.5 × 1013 m−3 (at the beginning of the mixing with antiprotons) resulted in, 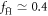 and ftrap ≃ 10−4. For similar conditions our results give
and ftrap ≃ 10−4. For similar conditions our results give 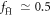 and ftrap ≃ 10−3, and further multiplication of ftrap by 0.13 (to account for the trap depth of 2 K in the simulations, compared to 0.5 K in the experiment) reduces this number to 1.3 × 10−4. This agreement is very good, considering the approximations involved, however we know of no experimental work where density or temperature effects are studied systematically for comparison with the trends observed here. We note that at high positron densities ne ≳ 1014 m−3, if narrow width (say around 0.1 mm radius)
and ftrap ≃ 10−3, and further multiplication of ftrap by 0.13 (to account for the trap depth of 2 K in the simulations, compared to 0.5 K in the experiment) reduces this number to 1.3 × 10−4. This agreement is very good, considering the approximations involved, however we know of no experimental work where density or temperature effects are studied systematically for comparison with the trends observed here. We note that at high positron densities ne ≳ 1014 m−3, if narrow width (say around 0.1 mm radius) 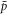 clouds are available, ftrap will be considerably enhanced. Given the increasing trend of ftrap as T is lowered, ongoing initiatives to produce colder positron clouds [33] are likely to prove beneficial.
clouds are available, ftrap will be considerably enhanced. Given the increasing trend of ftrap as T is lowered, ongoing initiatives to produce colder positron clouds [33] are likely to prove beneficial.
The range of densities and temperatures covered in this paper should also serve to inform other experiments, though some conditions may differ. Among the parameters we have not varied is the magnetic field strength. A stronger magnetic field will reduce the velocity vD of the antiprotons (see equation (3)), and thus counteract the radial reduction of the trapping rate in figure 2. Further, the radius of the positron plasma will also vary between different experiments. This could change the results quantitatively, but should not affect the trends we observe, as the underlying physics remains the same. Finally, it should be noted that we have assumed that the antiprotons are in thermal equilibrium with the positron plasma. In experiments, they have to be injected with some finite kinetic energy. Whether or not antihydrogen formation starts before the antiprotons thermalise will depend on the balance between the slowing rate and the three-body recombination rate. Such epithermal antihydrogen formation was discussed in [21].
Acknowledgements
SJ wishes to acknowledge the Swedish Research Council (VR) for financial support (grants nos. 2008-00442 and 2012-02435), and the High Performance Computing Center North (HPC2N) for computing resources. MC thanks the EPSRC (UK) for support of his antihydrogen work.